Aurora Institute
Blogs CompetencyWorks Blog A Mastery-Based Math Teacher’s Journey, Part 1 – Initial (mis)Steps and the “Aha!” Moment

A Mastery-Based Math Teacher’s Journey, Part 1 – Initial (mis)Steps and the “Aha!” Moment

CompetencyWorks Blog

Author(s): Ashley Ferrara

Issue(s): Issues in Practice, Rethink Instruction, Learn Lessons from the Field

This is the first post in a four-part series by Ashley Ferrara about her ongoing journey to develop a mastery-based approach to teaching mathematics. She is a teacher and interim acting assistant principal at the Academy for Software Engineering in New York City, a member school of the Mastery Collaborative.

When my school announced it was officially shifting to mastery-based learning, I called its bluff. We hadn’t shifted grading platforms, so I wrote it off as a firework that would fizzle in a year. (Not to mention that I believed mastery-based learning was completely impossible in a mathematics classroom. Had anyone seen the number of content standards I had to cover in a single school year?!)

Like clockwork, I continued with each of my algebra units having two quizzes and a cumulative unit test at the end—of course preceded by two days of review in class—and patiently waited to be told that we were no longer moving in that direction as a school. Well, my school called my bluff. Big time. The following year, we shifted fully to mastery-based learning (yes, including that grading platform I was holding out for), and I had to eat my words.

Is this the most politically correct way to start a blog series that cannot say enough in praise of mastery-based learning? Probably not, but I want you to know that if you are where I was at, I get you. I hear you. I was (and definitely sometimes still am) you. I did not come out of the educational womb pushing mastery-based learning, and it was a bumpy road to get here, but I’m really excited to share with you what I’ve learned along the way.

We are going to review my transition in shifts over four blog posts, because to say it was smooth, seamless, and quick would be an outright lie. Shifting to mastery-based learning is a multi-year process that I am very much still working on. The scope of the four blog posts is:

  1. Developing my initial mastery skill, and my “aha! moment” that mathematics repeats itself.
  2. How I taught and assessed mathematics content that did not repeat itself.
  3. My evolution to skills that could be assessed repeatedly throughout the year.
  4. How I transitioned entirely to a problem-solving approach and removed all content-specific language from my mastery skills.

The first shift was trying to identify what a mastery skill was in the world of algebra. To be honest, I’m going to more or less skip over that entire first year of transition and call it a loss. I was the definition of a “square peg, round hole” approach to mastery-based learning, and my first set of mastery skills couldn’t actually be called a set, because it never stayed the same. I was making token changes to a traditional unit—describing each of its parts in a sentence with a rubric, and the rubric changed weekly.

Below is an example of a mastery skill from my first year. It was created for my first unit, which focused on distance-time graphs. It falls into my “what not to do” category for many reasons, but the two most prominent reasons are noted in my takeaways below the skill.

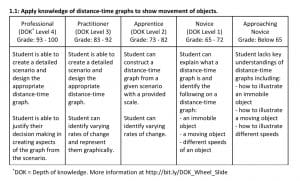
Table: Apply knowledge of distance-time graphs to show movement of objects

The biggest thing to celebrate about this was simply that I did it, so I would never again have to create my first mastery skill and rubric. I also had two major takeaways that influenced the discussions and decisions my co-teacher Stephanie Iovan and I made for the next school year:

  • Takeaway #1: If the mastery skill only appears in one unit within the course curriculum, you can only assess it during that unit.
  • Takeaway #2: If the mastery skill progresses just like your curriculum (i.e., teaching the skill at the Novice level at the beginning of the unit and at the Professional level at the end of the unit), you will not be able to fully assess the skill until the end of the unit.

Only assessing a skill once, at the end of the unit, corresponds to the “one and done” unit tests that mastery-based learning shifts away from. In later blog posts, I’ll cover how to create skills that can be repeatedly reassessed throughout both a unit and a school year.

Photo of Stephanie Iovan and Ashley Ferrara
Stephanie Iovan and Ashley Ferrara

Stephanie and I really started to make headway the second year, in large part due to what we had learned the first year. I remember a meeting we had over the summer to say, “we can’t do that again,” and really trying to hammer out some consistency between our skills. One thing I’m proud of that we developed was a set of three year-long mastery skills:

  • MS1: I can create the appropriate domain and range given any representation.
  • MS2: I can graph any function (linear, quadratic, exponential, absolute value, piecewise).
  • MS3: I can isolate any variable.

At the time, I was just excited to have something on the page that we could stick with for longer than 72 hours. But in hindsight, this was a really important moment in the mastery journey: we had identified that mathematics repeats itself. You may be saying “duh,” but for us, having come right out of a traditional format where every unit feels completely different from the rest, this was huge. We found a way to create a throughline for our students for the year-long course.

With this, I leave you with your first piece of homework as a teacher thinking about mastery within your classroom: What is your throughline? What big ideas repeat consistently throughout the year? Think big, think little—this is messy stuff! But try to get at least two topics that repeat themselves in your course(s) and write them down. We’ll talk more about identifying patterns and trends in the next post.

Learn More:

Ashley Ferrara is a founding faculty member at the Academy for Software Engineering (AFSE), a public high school in New York City. She joined AFSE nine years ago and was an Early Career Fellow and Master Teacher with Math for America for seven of those years. After earning a bachelor’s degree in accounting from the University of Connecticut and working with a big-four accounting firm, she earned master’s degrees in mathematics education from Teachers College, Columbia University and educational leadership and administration from Bank Street College of Education. She also graduated from the New York City Department of Education’s Leaders in Education Apprenticeship Program (LEAP).